3. Complex numbers

Why?

Complex numbers are generally used in engineering, electrical engineering and quantum mechanics. They provide a system for finding the roots of polynomials used in theoretical models for the investigation of electrical current, wavelength, liquid flow in relation to obstacles, dynamos and electric motors, and the manipulation of the matrices used in modelling.

What?

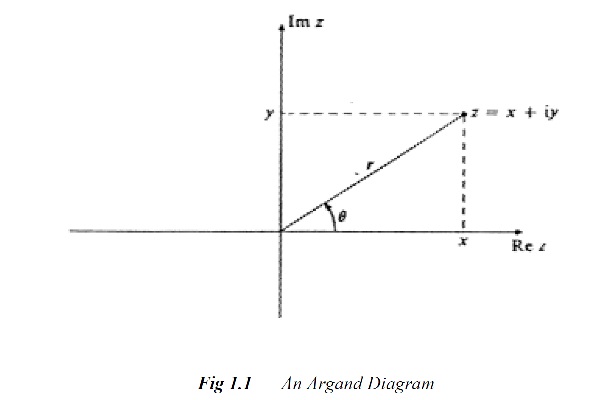
The complex number z = x + iy can also be written in modulus argument form

The real part, Re z = x = r cos θ and the imaginary part, 1mz = y = r sin θ. Complex numbers can be shown as points on an Argand diagram.

Standard rules exist defining, addition, subtraction, multiplication and divisions of complex numbers.

We can show that there exists the following convenient alternative form of equation (2.1):

Just as a series expansion for exp (x) was calculated, (equation (1.2)), so we can write down the series for exp (iθ) as

Taking the real and imaginary parts we get:

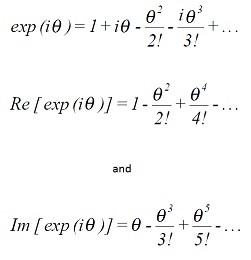
Comparison with equations (1.3) and (1.4) gives us that

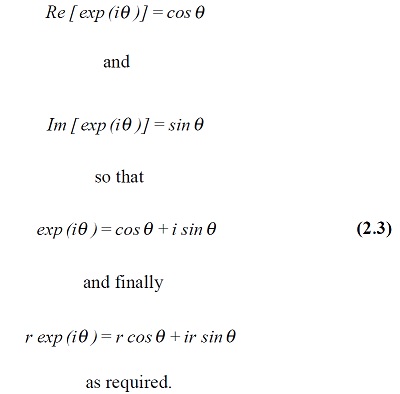
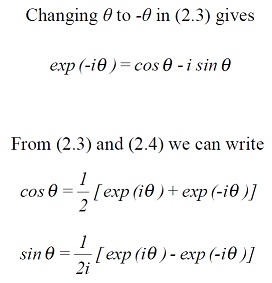
From (2.2) complex numbers are straightforward to multiply:

By extension, for z with unit modulus,

This is de Moivre's theorem. It is often written in the alternative form:

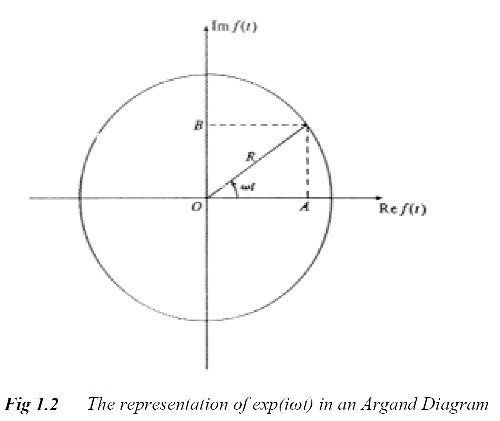
Equation 2.2 also provides a very useful framework for the analysis of periodic systems.
For example, if θ = ωt, where ω is an angular velocity, then the function

has real and imaginary parts which undergo sinusoidal variations with amplitude R and
period 2π/ω (although out of phase by π/2).