5. State Space Analysis

Why?

This brief note is simply to introduce the concept of state space analysis so that you will recognise the terminology. You will not be expected to apply this approach yourselves.

What?

Fundamentally, state space analysis is a rewriting of the equations of motion (or more generally equations describing an arbitrary system) in terms of first order differential equations. The dependent variables of these equations are known as the state variables. For an nth order system (nth order DE) there will result n first order equations and so there will be n state variables needed to describe the system. The decomposition into first order DEs is not unique and neither therefore is the choice of state variables. Often the choice will be determined by pragmatism (ie a simpler set of equations results) or physical meaning (ie the state variables have a clear physical interpretation). 

A vector, having as its components the state variables (which are functions of time), is known as the state vector. At any time it represents the state of the system. 

Once the initial state is known together with the inputs, the state of the system for all future times can be calculated.

The mathematical space which encompasses all possible values of the state vector is known as the state space; hence the term: state space analysis. The dimension of the state space is the order of the system. Take for example the mass-spring-damper equation (3.13). This can be written as a pair of first order DEs:

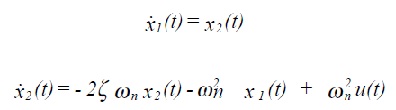
where x1(t) ≡ x(t) , the position at time t and x2 (t) ≡ x!(t), the velocity at time t. The variables x(t)and x!(t)are the state variables; they completly describe the system.

The pair of equations can be written in matrix notation as follows:

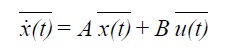
where x(t)is the state vector and

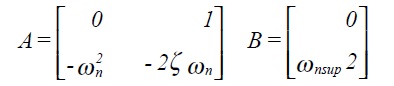
and u(t) is the forcing vector.

An advantage of state space analysis, in contrast to transfer function analysis, is that it can be extended from single input-single output systems to multi-variable systems with many inputs and outputs and also that it can deal with non-linear systems.