6. Fourier Transform and Spectral Density Functions

Why?

These notes are simply to assist you in understanding what a spectral density function is. You will not be expected to manipulate such functions, but they are a handy way to represent wind speed variation (as in Wind I and Wind II modules).

What?

Harmonic functions

Harmonic functions (written as eiωt or cos (ωt)) are attractive from an analytical point of view for a number of reasons: they are straightforward to differentiate, integrate and multiply; moduli are easily evaluated and each contains only one frequency. The last property will be found to be useful in the context of analysing systems which are characterised by a fundamental (resonance) frequency. Complexity can be dealt with through superposition.

Technically, the harmonic functions can be shown to the mutually orthogonal and complete (any reasonable function can be expressed as a linear combination of them). If the period of f(t) is T, then mutual orthogonality means

If we take f(t) = cos (2πnt/T) with integer n, it can be shown to be orthogonal by integrating
over the range (-T/2, T/2).

Since cos (2πnt/T) is an even function, linear combinations will always be even.

A more general set of functions is then required to give completeness. As a function can be
expressed as the sum of an even and an odd part, the suggested set of functions is:

for integers n and m. 

It is straightforward to show that the orthogonal property still applies.

A particular linear combination of the above set (which also has the desired properties) is

This is attractive in that it can be written as simply exp (i 2πnt/T).

Fourier series

A Fourier series is an expansion of a function in terms of its Fourier components as suggested by the above discussion.

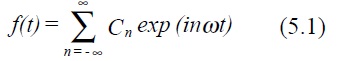
The constants Cn are known as the Fourier coefficients, ω = 2π/T is the fundamental
frequency.

If a function f(t) is known, the Fourier components can be projected out by pre-multiplying
by exp (-im ωt) and integrating from -T/2 to T/2.

Fourier series can be differentiated and integrated term by term.