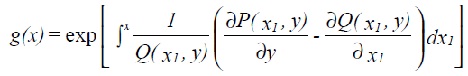The general first-order equation can be written as

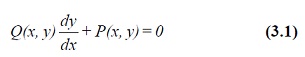
If the equation can be rewritten in the form

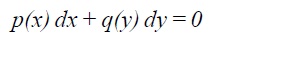
the variables are said to be separated and the solution is given trivially as

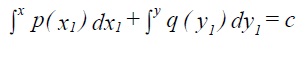
Generally this will not be the case. The solution sought can be written as

Differentiating this with respect to x gives

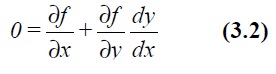
By comparison with the original equation (3.1) we get

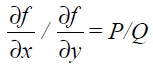
If the original equation (3.1) pre-multiplied by a function g(x, y) is to result in the form given by (3.2) then

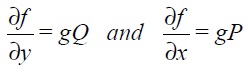
since

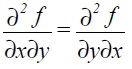
we get

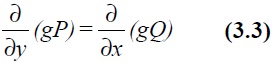
For the particular case of g (x, y) constant the original differential equation is known as exact and the solution can be written down as

where the function h(y) is chosen so that

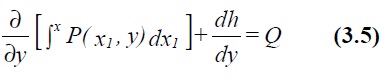
Alternatively the solution

where

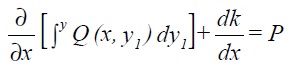
may be easier to evaluate.

If the equation is not exact, an integrating factor g (x, y) must be found. Expanding equation (3.3) gives

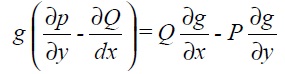
If P is substituted from the original equation we get an equation for g:

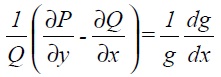
For common occurring cases where the LHS of (3.5) is a function of x only the solution can be obtained directly by integration as