Maths
1. Why do I need maths?
2. Taylor series
3. Complex numbers
4. Differential equations and Laplace transform
5. State space analysis
6. Fourier transform and spectral density functions
7. Matrices and Eigen value analysis
8. Statistics and applied probability
4. Differential Equations and the Laplace Transform
4.2. Second-order equations
Second-order equations occur frequently in the description of dynamical systems with springs, damping and inertial forces. Very often these will also be linear. The general case of importance is
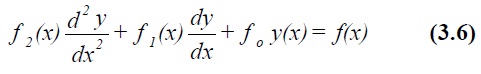
where, in dynamic analysis, f(x) on the RHS is the forcing function. A special case has f(x) = 0. A solution of (3.6) is known as the particular function, whilst a solution of (3.6) with f(x) = 0 is called the complementary function. The general solution of (3.6) is the sum of these two. Solutions of (3.6) are often of the form
![]()
where λ1 , λ2 and c are fixed numbers and A and B the two arbitrary constants to be fixed through application of the boundary conditions. For many dynamic systems (3.6) can be further simplified so that f0, f1 and f2 become constants, ie
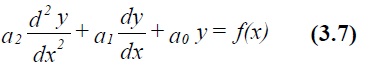
If f(x) is zero or takes a simple form we can proceed as follows. Assume the complementary function is of the form
![]()
This results in
![]()
which is clearly satisfied if
![]()
This expression, known as the auxiliary equation, is solved to give λ (two solutions in general) λ1 and λ2
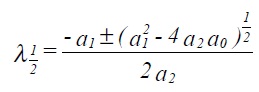
Since the differential equation (3.7) with f(x) = 0 is linear we can write down the complementary function (in this case the general solution for f(x) = 0) as
![]()
