Why?

You will not have to use Taylor Series yourselves, but it is a common way in which useful approximations are generated (eg that sinq can be approximated by q for small angles). There are occasions when lecturers will use this to provide a simpler formulation (eg expressions relating to extreme winds in the Wind II module).

What?

If a function f(x) is differentiable up to nth order in some neighbourhood of a point x = a, then in the neighbourhood, the function can be represented by a power series in (x - a).

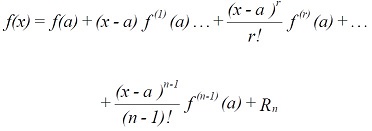
For many functions the remainder term Rn → 0 as n → ∞, and so we can write

                                                                                                                (1.1)

This series expansion is known as the Taylor series. For the case of a = 0 it is known as the Maclaurin's series.

Some important series easily derived are for the exponential, cosine and sine functions.

Series expansions are widely used in engineering to provide approximations to functions.Sufficient accuracy is often achieved by taking just the first two terms of the series. If (x - a) < < 1 then higher powers will contribute little.

Say we wish to express the value of a function for small displacements h from an operating point a. Then h = x - a and equation (1.1) becomes

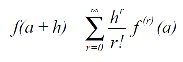
Taking just the first two terms (sometimes referred to as linearisation) gives

If we take as an example f(x) = xn, then

and it is clear that all powers of h greater than 1 have been discarded. Provided h < < 1 such approximations are reasonably accurate.